话说这离散数学，犹如一亩三分地，里面长满了奇花异草，偏序集合便是其中一朵。哦，别误会，我可不是来给你科普的，要真那么好心，我早去开直播讲相声了。今日，咱就以一种杠精的姿态，来看看这个所谓的偏序集合，究竟是个什么鬼。

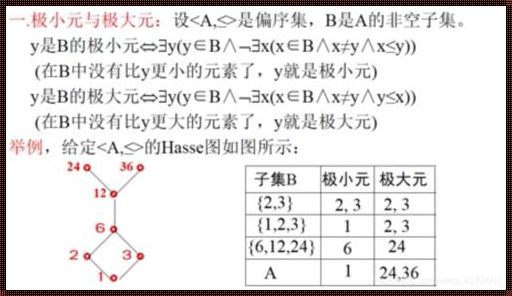
首先，得给偏序集合下个定义，免得你们说我糊弄事儿。偏序，偏序，顾名思义，就是不全有序。嘿，别瞪眼，我真不是在绕弯子。在离散数学这个大染缸里，偏序集合可是一种关系，能让一堆元素看似有序，实则不然。这种关系，比那塑料姐妹花还虚假。

好了，废话少说，切入正题。怎么判断一个集合是不是偏序呢？这时候，你得瞪大眼睛，看清楚关系是不是满足三个条件：自反性、反对称性和传递性。别看这三个条件挺唬人的，其实说白了，就是让你看看这个关系是不是有“自知之明”，以及有没有“挑拨离间”的本事。

先说自反性。自反性就是集合里的每个元素都和自己有关系。这就好比一个人，得先认识自己，才能去认识别人。如果集合里有个元素，它愣是和自己没关系，那这个集合就不是偏序的。这么一说，是不是觉得这自反性还挺有人情味的？

再来看反对称性。反对称性就是如果元素A和元素B有关系，而元素B和元素A也有关系，那A和B必须是同一个元素。这听起来是不是像那句“我爱你，你爱我，我们俩是同一人”？不过，在偏序集合里，这种情况可是要不得的，否则就破坏了反对称性。

最后是传递性。传递性就是如果元素A和元素B有关系，元素B和元素C也有关系，那么元素A和元素C也必须有关系。这就像病毒传播，一旦沾染，必定蔓延。不过，在偏序集合里，这种传递性可是关系稳定的保障。

归纳起来说，你可能会问：“这三个条件到底有啥用？”嘿，这三个条件可是判断偏序集合的“金标准”。只要你的集合里的关系满足这三个条件，恭喜你，发现了一个偏序集合。要是缺了一个，那对不起，你的集合只能算是“伪君子”。

当然，离散数学的世界里，偏序集合只是冰山一角。在这个舞台上，还有无数诡异的现象等着我们去探索。而今天，咱们就先聊到这里，毕竟，饭要一口一口吃，事儿要一件一件做。下次，我们再一起杠一杠离散数学的其他诡异现象。